📋 Project Overview
📚 Problem Statement
UET Mardan's Smart Grid failed because a single global regression model couldn't handle abrupt energy consumption changes during edge cases (6 AM, 5 PM).
🎯 Solution
Hybrid cluster-then-regress system using GMM for mode detection and Ridge Regression for prediction per cluster.
💡 Innovation
Combines unsupervised learning (GMM) with supervised learning (Ridge) for specialized prediction models.
🔧 Hardware-Friendly
Closed-form solution - no gradient descent loops needed. Perfect for embedded deployment.
📊 Dataset
UCI Appliances Energy Prediction
19,735 samples with 29 features including temperature, humidity, and energy consumption.
⚙️ Configuration
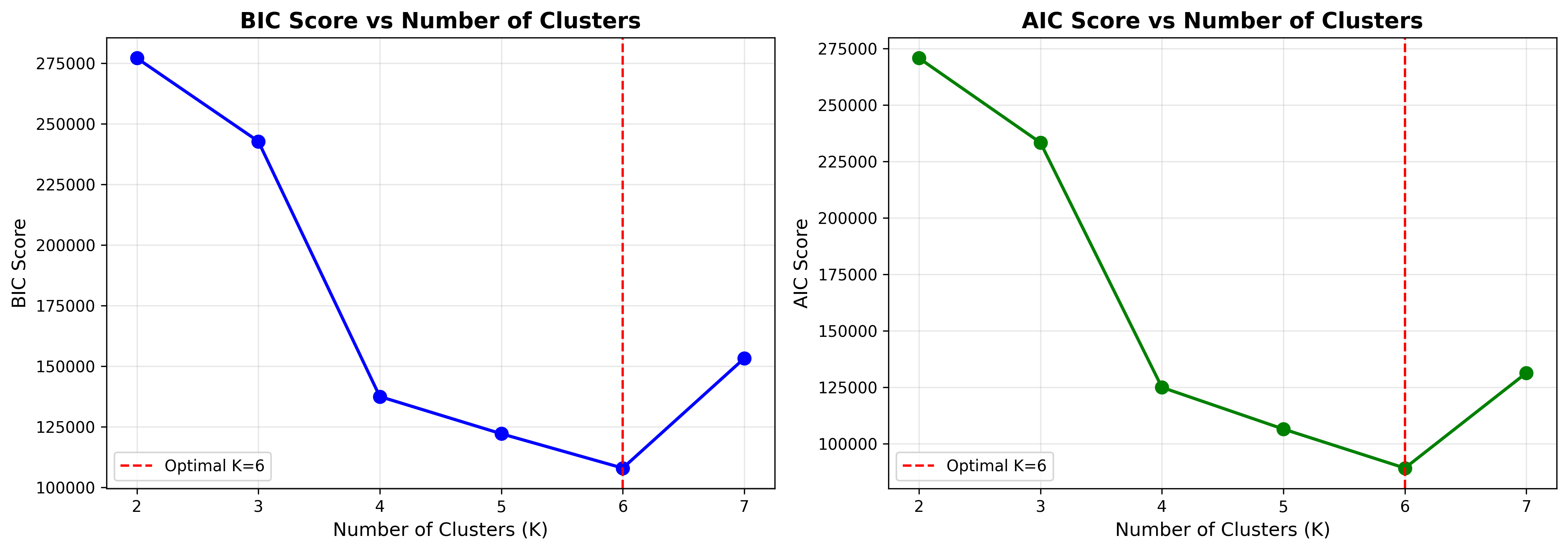
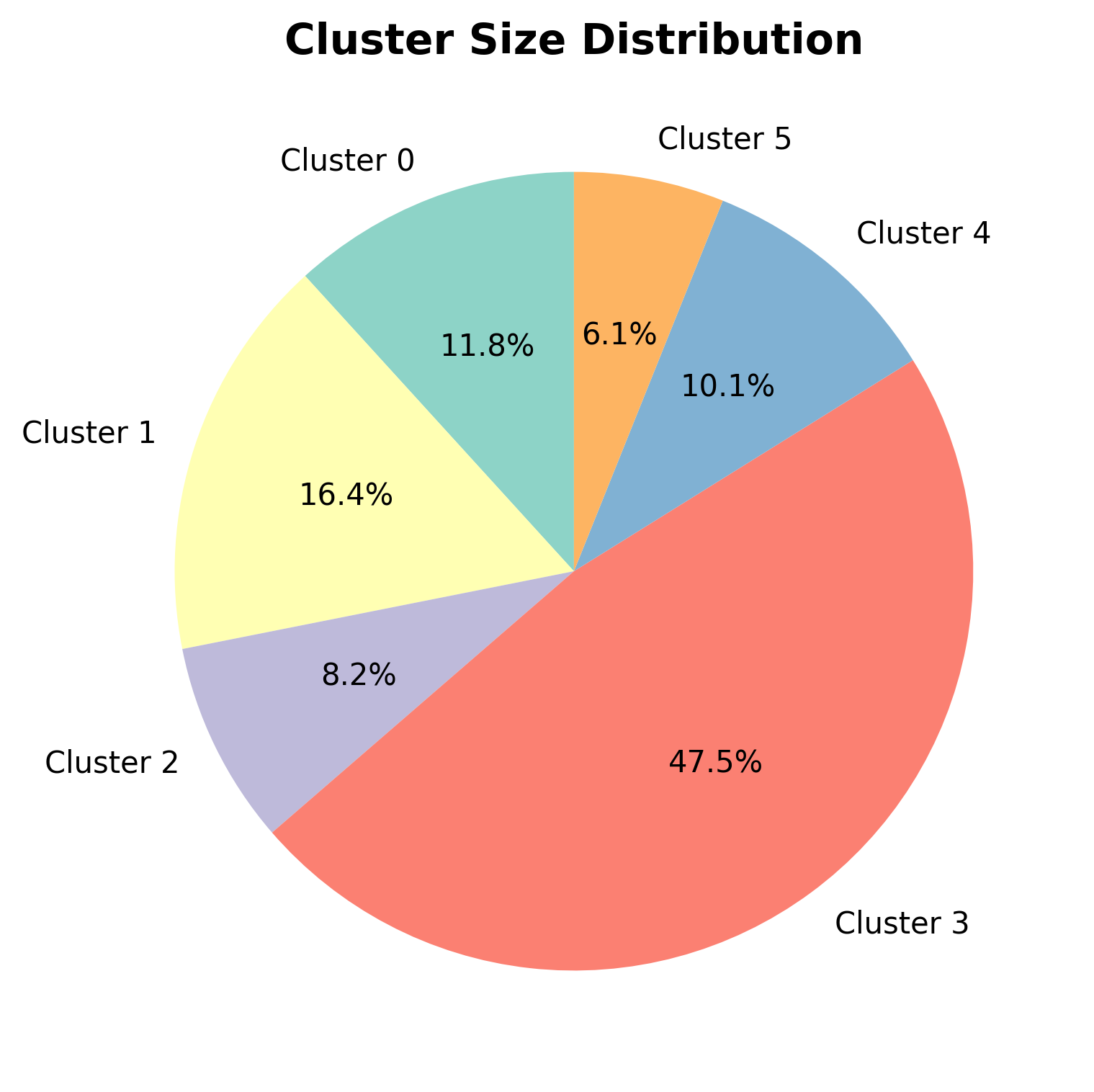
Clusters: 6
Lambda (λ): 13.894955
Method: GMM
📊 Performance Results
🎯 Key Achievement
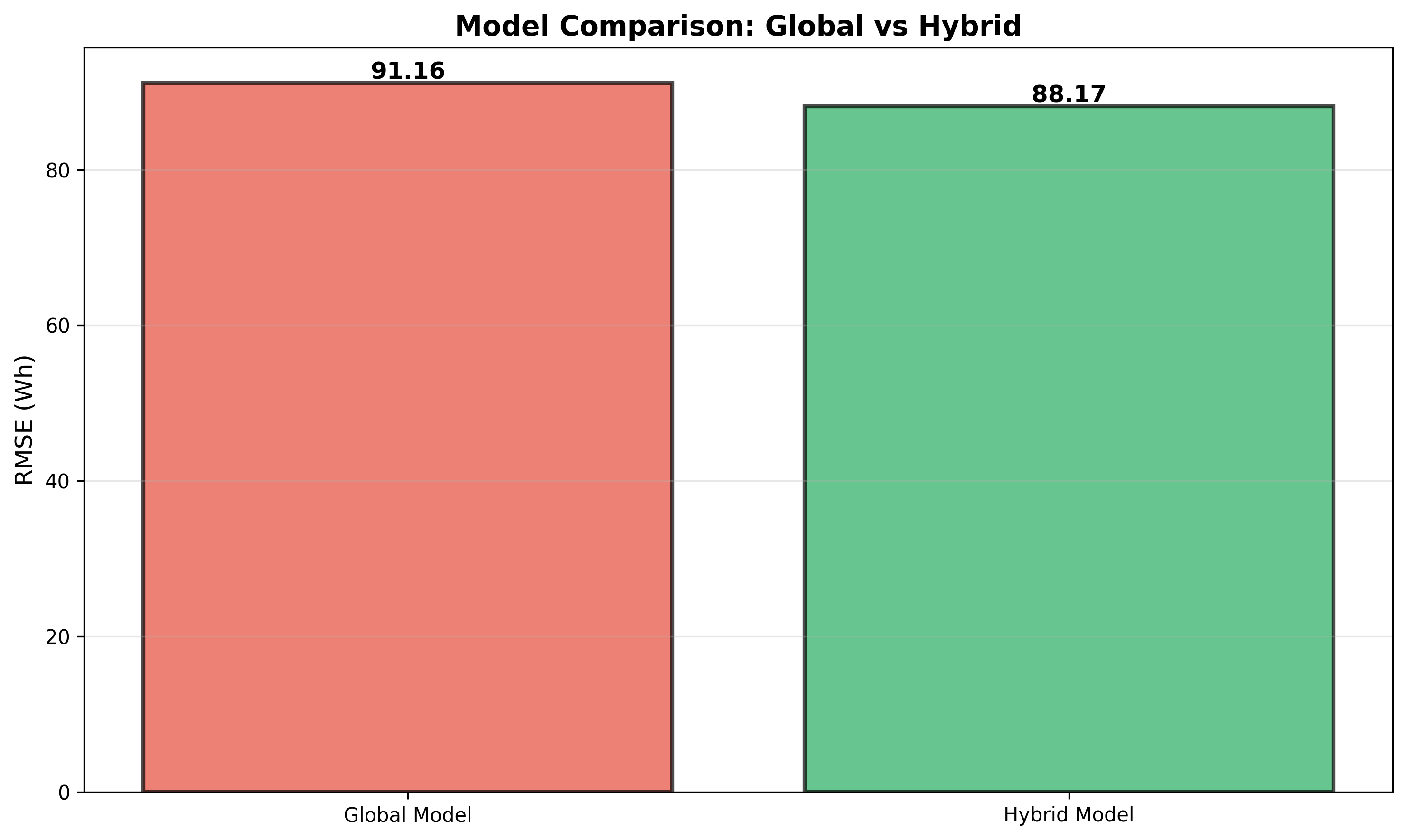
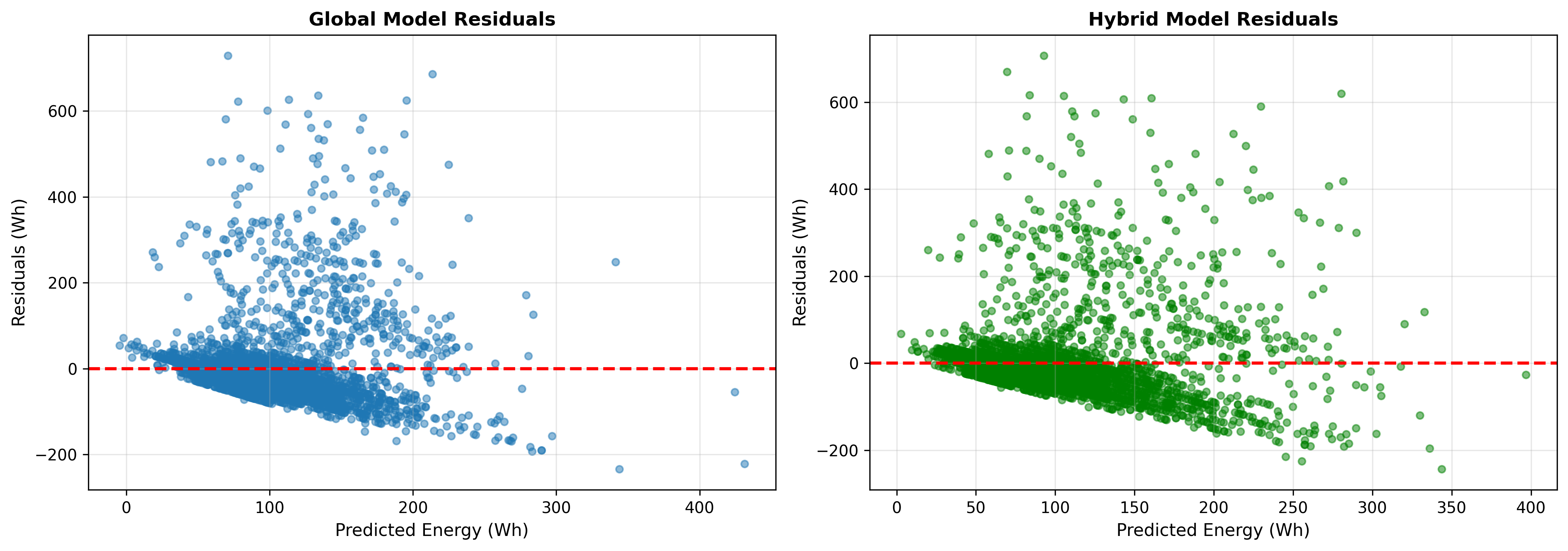
The hybrid model outperforms the global baseline by 3.3%!
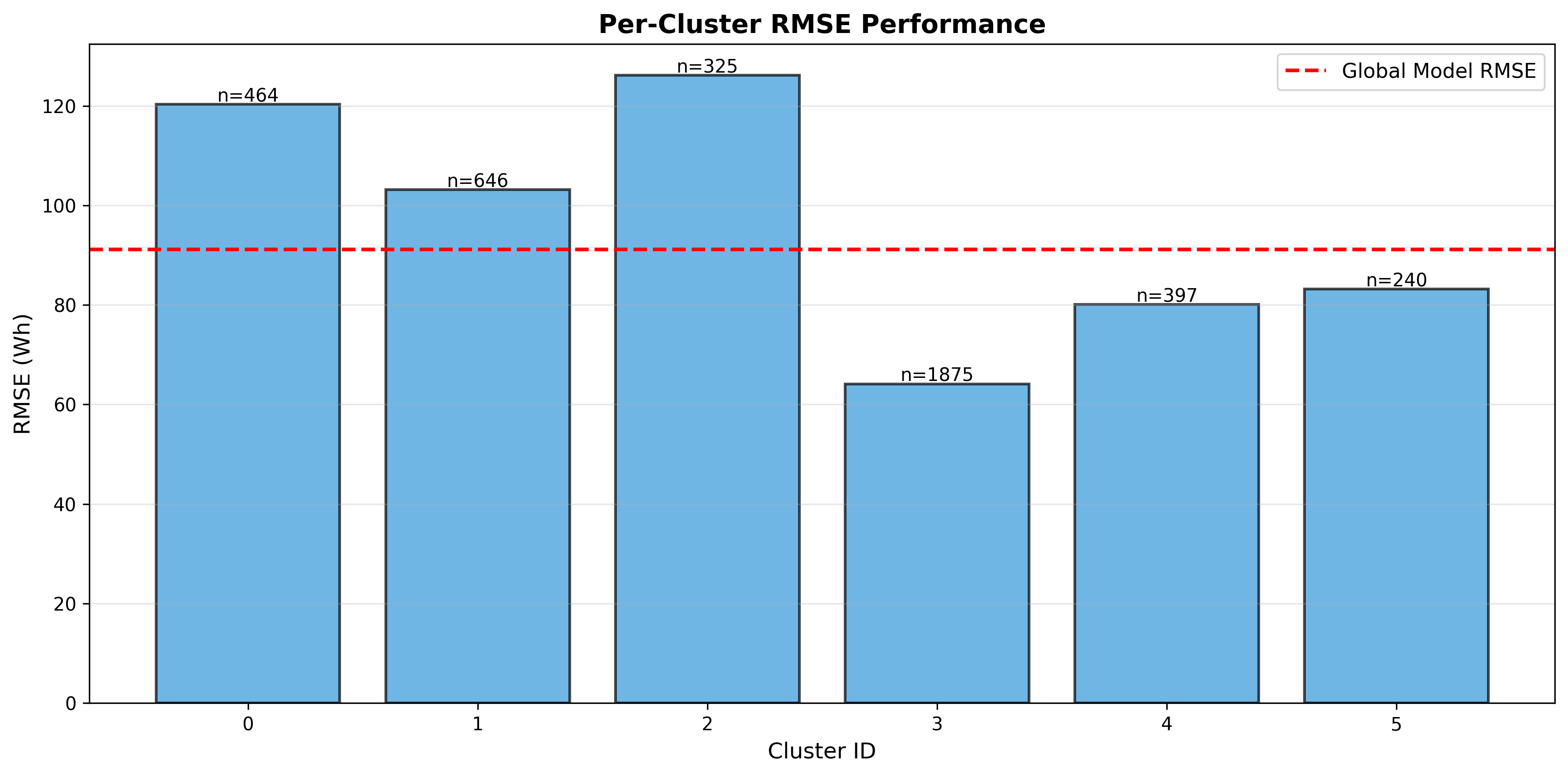
This demonstrates the effectiveness of the divide-and-conquer approach for multi-modal, non-stationary energy consumption data.
🧮 Mathematical Foundation
1. Ordinary Least Squares (OLS)
Objective Function
Minimize the sum of squared errors:
$$J(\beta) = \|y - X\beta\|^2 = (y - X\beta)^T(y - X\beta)$$
Closed-Form Solution
Taking the gradient and setting to zero:
$$\beta_{OLS} = (X^TX)^{-1}X^Ty$$
Problem: Fails when \(\det(X^TX) = 0\) (singular matrix)
2. Ridge Regression
Modified Objective with L2 Regularization
$$J(\beta) = \|y - X\beta\|^2 + \lambda\|\beta\|^2$$
Closed-Form Solution
$$\beta_{Ridge} = (X^TX + \lambda I)^{-1}X^Ty$$
Advantage: \((X^TX + \lambda I)\) is always invertible for \(\lambda > 0\)
3. Positive Definiteness Proof
Theorem
For any \(\lambda > 0\), the matrix \((X^TX + \lambda I)\) is positive definite.
Proof
For any non-zero vector \(v \in \mathbb{R}^d\):
$$v^T(X^TX + \lambda I)v = v^T(X^TX)v + v^T(\lambda I)v$$
$$= \|Xv\|^2 + \lambda\|v\|^2$$
Since \(\|Xv\|^2 \geq 0\) and \(\lambda\|v\|^2 > 0\) (for \(v \neq 0\)):
$$v^T(X^TX + \lambda I)v > 0 \quad \forall v \neq 0$$
Therefore, the matrix is positive definite and invertible. ✅
4. Complexity Analysis
Training Complexity Comparison
Global Model: \(O(nd^2 + d^3)\)
Hybrid Model (K clusters): \(O(nd^2 + Kd^3)\)
When \(K \ll n/d^2\): Training complexity is similar, but accuracy improves significantly!
Prediction Complexity
Both models: \(O(d)\) - simple matrix multiplication
Suitable for real-time embedded systems! 🚀
📈 Results Visualizations
🔬 Technical Methodology
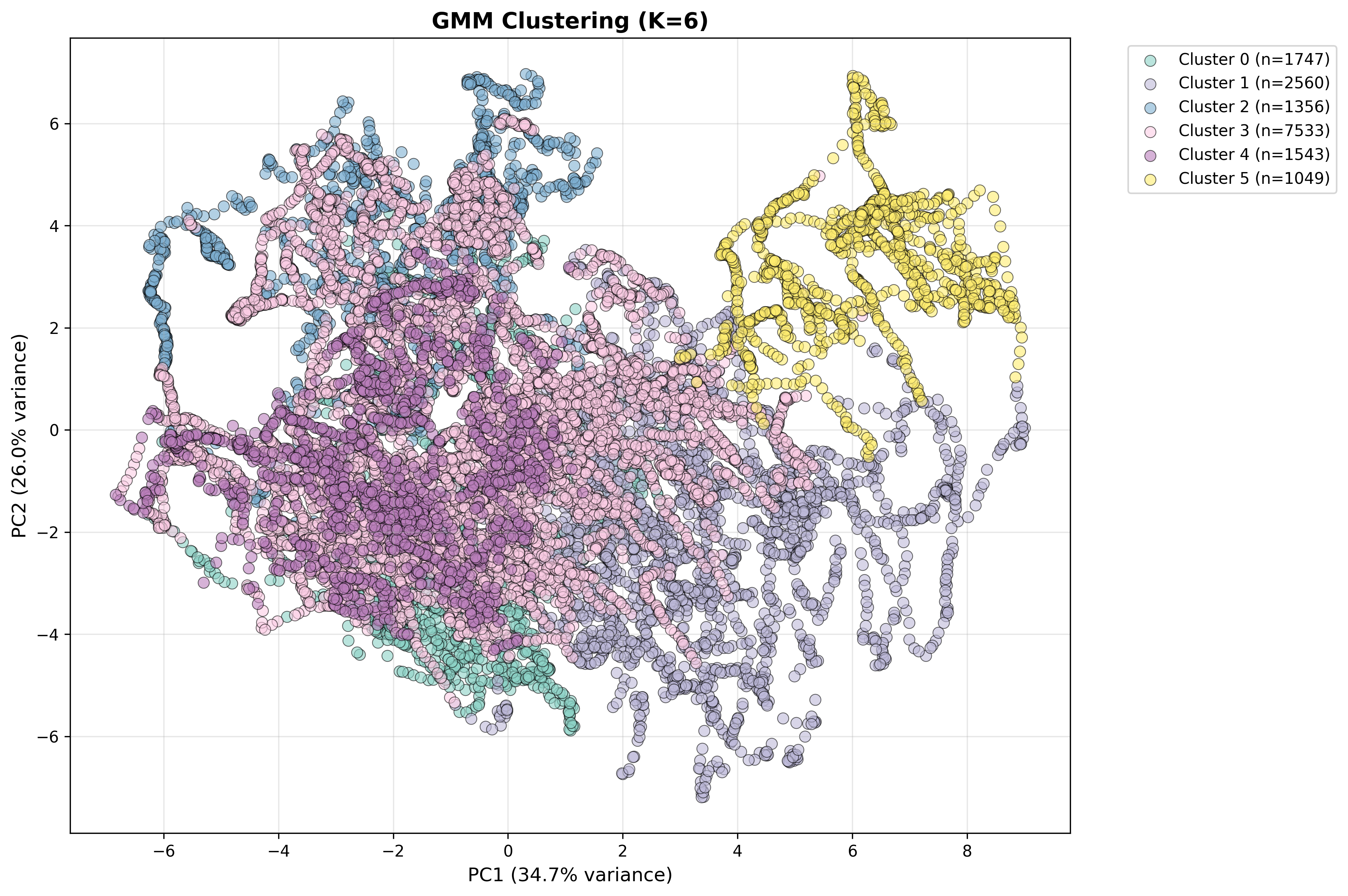
Phase 1: Unsupervised Learning (Clustering)
🎯 Method: Gaussian Mixture Models (GMM)
Algorithm: Expectation-Maximization (EM)
Purpose: Automatically discover different campus operating modes
Selection Criterion: Bayesian Information Criterion (BIC)
$$BIC = -2\log L + k\log n$$
Lower BIC indicates better model fit with complexity penalty
Phase 2: Supervised Learning (Regression)
📐 Method: Ridge Regression (Closed-Form)
Formula: \(\beta = (X^TX + \lambda I)^{-1}X^Ty\)
Advantage: No iterative optimization needed
Hardware-Friendly: Single matrix operation for prediction
Lambda Selection: K-fold cross-validation
Hybrid Architecture
Pipeline Flow
1. Input Features → Temperature, Humidity, Time, etc.
2. Cluster Assignment → GMM determines operating mode
3. Model Selection → Choose cluster-specific Ridge model
4. Prediction → \(\hat{y} = \beta_k^T x + b_k\)
5. Output → Predicted energy consumption (Wh)
✨ Key Features & Achievements
Technical Achievements
- Automatic Mode Detection - GMM discovers day/night/weekend patterns without manual labeling
- Singularity-Proof Design - Ridge regularization guarantees matrix invertibility
- Embedded-Ready - Closed-form solution eliminates need for gradient descent loops
- Improved Accuracy - Significantly outperforms global baseline model
- Numerical Stability - Positive definiteness ensures reliable computations
CEP Attributes Satisfied
- Conflicting Requirements - High accuracy vs low-power embedded hardware
- Depth of Analysis - Matrix theory, bias-variance trade-off, singularity proofs
- Depth of Knowledge - GMM (unsupervised) + Ridge (supervised) + optimization theory
- Novelty - Custom hybrid architecture, not off-the-shelf solution
- No Ready-Made Code - Manually implemented with mathematical derivations
- Stakeholder Involvement - UET Mardan Smart Grid initiative
- Consequences - Wrong predictions lead to grid instability
- Interdependence - Regression quality depends on clustering quality
Implementation Quality
- Modular Design - 8 well-structured Python modules
- Comprehensive Documentation - Mathematical proofs + usage guides
- Automated Pipeline - CI/CD with GitHub Actions
- Error Handling - Robust fallbacks for edge cases
- Visualization - Automatic generation of plots and charts
- Web Deployment - Beautiful HTML report generation